kspace.hpp File Reference

K-space (Fourier space) helper functions for spectral methods. More...

#include <array>
#include <cmath>
#include <openpfc/constants.hpp>
#include <openpfc/core/world.hpp>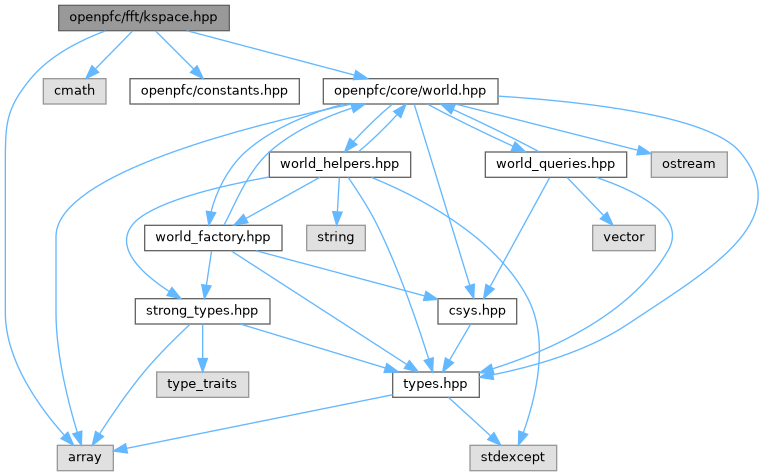

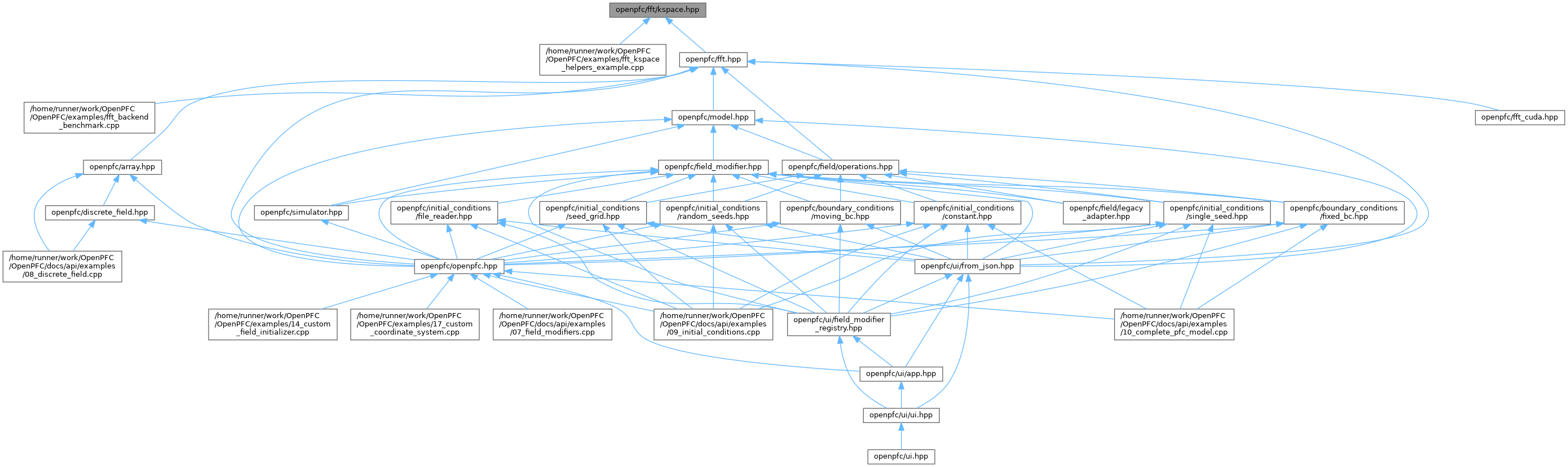
Include dependency graph for kspace.hpp:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
template<typename T >
std::array< double, 3 >	pfc::fft::kspace::k_frequency_scaling (const world::World< T > &world) noexcept
	Compute frequency scaling factors for each dimension.
double	pfc::fft::kspace::k_component (int index, int size, double freq_scale) noexcept
	Compute k-space wave vector component with Nyquist folding.
double	pfc::fft::kspace::k_laplacian_value (double ki, double kj, double kk) noexcept
	Compute Laplacian operator value -k² in Fourier space.
double	pfc::fft::kspace::k_squared_value (double ki, double kj, double kk) noexcept
	Compute squared magnitude k² = k_x² + k_y² + k_z².

Detailed Description

K-space (Fourier space) helper functions for spectral methods.

This file provides zero-cost helper functions for computing wave vector components in Fourier space for FFT-based spectral methods. These functions encapsulate the standard frequency scaling and Nyquist folding logic that is duplicated across 120+ lines in multiple examples.

The problem: Every spectral method example contains the same 30-line pattern:

// Duplicated in 04_diffusion_model.cpp, 12_cahn_hilliard.cpp, etc.
double pi = std::atan(1.0) * 4.0;
double fx = 2.0 * pi / (spacing[0] * size[0]);
double fy = 2.0 * pi / (spacing[1] * size[1]);
double fz = 2.0 * pi / (spacing[2] * size[2]);
for (int k = o_low[2]; k <= o_high[2]; k++) {
  for (int j = o_low[1]; j <= o_high[1]; j++) {
    for (int i = o_low[0]; i <= o_high[0]; i++) {
      double ki = (i <= size[0] / 2) ? i * fx : (i - size[0]) * fx;
      double kj = (j <= size[1] / 2) ? j * fy : (j - size[1]) * fy;
      double kk = (k <= size[2] / 2) ? k * fz : (k - size[2]) * fz;
      double kLap = -(ki * ki + kj * kj + kk * kk);
      // ... use kLap ...
    }
  }
}

The solution: Extract reusable helpers:

auto [fx, fy, fz] = k_frequency_scaling(world);
for (int k = o_low[2]; k <= o_high[2]; k++) {
  for (int j = o_low[1]; j <= o_high[1]; j++) {
    for (int i = o_low[0]; i <= o_high[0]; i++) {
      double ki = k_component(i, size[0], fx);
      double kj = k_component(j, size[1], fy);
      double kk = k_component(k, size[2], fz);
      double kLap = k_laplacian_value(ki, kj, kk);
      // ... use kLap ...
    }
  }
}

All functions are inline, noexcept, and zero-cost abstractions that compile to identical machine code as the manual implementation.

See also

core/world.hpp for World coordinate system

fft.hpp for FFT interface

constants.hpp for mathematical constants (two_pi)

Author

OpenPFC Contributors

Date

2025-11-23

Function Documentation

k_component()

double pfc::fft::kspace::k_component ( int  index, int  size, double  freq_scale  )

inlinenoexcept

Compute k-space wave vector component with Nyquist folding.

Converts a grid index to the corresponding wave vector component, handling the Nyquist frequency folding that occurs in real-to-complex FFTs.

FFT convention:

• Indices 0 to size/2: Positive frequencies k = index * freq_scale
• Indices > size/2: Negative (aliased) frequencies k = (index-size) * freq_scale

Parameters

index	Grid index (0 to size-1)
size	Domain size in this dimension
freq_scale	Frequency scaling factor (from k_frequency_scaling)

Returns

Wave vector component in rad/unit_length

Note

This is a zero-cost abstraction (inline, noexcept)

Handles both positive and negative frequencies correctly

Replaces: double ki = (i <= size / 2) ? i * fx : (i - size) * fx;

int Lx = 128;
double fx = two_pi / (0.1 * Lx);
 
double k0 = k_component(0, Lx, fx);      // 0.0 (DC component)
double k1 = k_component(1, Lx, fx);      // 1*fx (first mode)
double k64 = k_component(64, Lx, fx);    // 64*fx (Nyquist)
double k127 = k_component(127, Lx, fx);  // -1*fx (negative)

Time complexity: O(1) Space complexity: O(1)

Here is the call graph for this function:

Here is the caller graph for this function:

k_frequency_scaling()

template<typename T >

std::array< double, 3 > pfc::fft::kspace::k_frequency_scaling ( const world::World< T > &  world )

inlinenoexcept

Compute frequency scaling factors for each dimension.

Calculates f = 2π / (spacing * size) for each dimension, which converts grid indices to wave vector components in Fourier space.

In spectral methods using FFT, derivatives in real space become multiplications by wave vectors in Fourier space. The frequency scaling establishes the relationship between grid indices and physical wave numbers.

Template Parameters

T	World coordinate system type (e.g., CartesianTag)

Parameters

world

Simulation world containing grid size and spacing

Returns

Array of frequency scaling factors [fx, fy, fz] in rad/unit_length

Note

This is a zero-cost abstraction (inline, noexcept)

Works correctly for 1D, 2D, and 3D domains

Replaces: double fx = 2.0 * pi / (spacing[0] * size[0]);

auto world = world::uniform(128, 0.1);
auto [fx, fy, fz] = k_frequency_scaling(world);
// fx = fy = fz = 2π / (0.1 * 128) ≈ 0.490873...

Time complexity: O(1) Space complexity: O(1)

Here is the call graph for this function:

Here is the caller graph for this function:

k_laplacian_value()

double pfc::fft::kspace::k_laplacian_value ( double  ki, double  kj, double  kk  )

inlinenoexcept

Compute Laplacian operator value -k² in Fourier space.

Calculates -(k_x² + k_y² + k_z²), the Fourier representation of the Laplacian operator ∇². Used in diffusion, heat, and phase-field equations.

Mathematical relationship:

• Real space: ∇² = ∂²/∂x² + ∂²/∂y² + ∂²/∂z²
• Fourier space: ∇² ↔ -k² = -(k_x² + k_y² + k_z²)

The negative sign is conventional, making the Laplacian negative definite.

Parameters

ki	Wave vector x-component
kj	Wave vector y-component
kk	Wave vector z-component

Returns

Laplacian operator value -k² ≤ 0

Note

This is a zero-cost abstraction (inline, noexcept)

Returns negative value for non-zero k

Returns exactly 0.0 for DC component (ki=kj=kk=0)

Replaces: double kLap = -(ki * ki + kj * kj + kk * kk);

// Diffusion equation: ∂u/∂t = D∇²u
// In Fourier space: ∂û/∂t = D(-k²)û
double ki = k_component(i, Lx, fx);
double kj = k_component(j, Ly, fy);
double kk = k_component(k, Lz, fz);
double kLap = k_laplacian_value(ki, kj, kk);
 
// Implicit time stepping
opL[idx] = 1.0 / (1.0 - D * dt * kLap);

Time complexity: O(1) Space complexity: O(1)

Here is the call graph for this function:

Here is the caller graph for this function:

k_squared_value()

double pfc::fft::kspace::k_squared_value ( double  ki, double  kj, double  kk  )

inlinenoexcept

Compute squared magnitude k² = k_x² + k_y² + k_z².

Calculates the positive squared magnitude of the wave vector, useful for higher-order operators, filtering, and wave number magnitudes.

Mathematical relationships:

• k² = k_x² + k_y² + k_z² = |k|²
• |k| = √k² (wave number magnitude)
• Biharmonic: ∇⁴ ↔ k⁴ = (k²)²
• Related to Laplacian: k_laplacian_value(ki, kj, kk) = -k_squared_value(ki, kj, kk)

Parameters

ki	Wave vector x-component
kj	Wave vector y-component
kk	Wave vector z-component

Returns

k² = k_x² + k_y² + k_z² ≥ 0

Note

This is a zero-cost abstraction (inline, noexcept)

Returns positive value (magnitude squared)

Replaces: double k2 = ki * ki + kj * kj + kk * kk;

double ki = k_component(i, Lx, fx);
double kj = k_component(j, Ly, fy);
double kk = k_component(k, Lz, fz);
 
double k2 = k_squared_value(ki, kj, kk);
double k_mag = std::sqrt(k2);  // Wave vector magnitude
double k4 = k2 * k2;  // Biharmonic operator

Time complexity: O(1) Space complexity: O(1)

Here is the call graph for this function:

Here is the caller graph for this function: